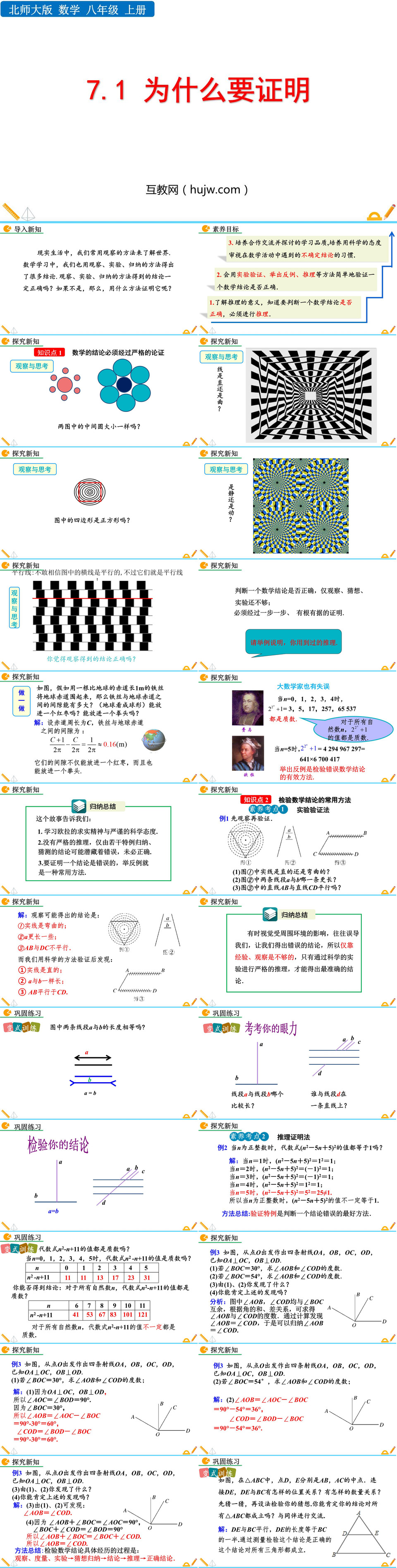
北师大版八年级数学上册《为什么要证明》平行线的证明PPT免费下载，共34页。素养目标1.了解推理的意义，知道要判断一个数学结论是否正确，必须进行推理．2. 会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确．3. 培养合作交流并探讨的学习品质,培养用科学的态度审视在数学活动中遇到的不确定结论的习惯.探究新知数学的结论必须经过严格的论证平行线:不敢相信图中的横线是平行的,不过它们就是平行线!判断一个数学结论是否正确，仅观察、猜想、实验还不够；必须经过一步一步、有根有据的证明.归纳总结这个故事告诉我们：1.学习欧拉的求实精神与严谨的科学态度.2.没有严格的推理，仅由若干特例归纳、猜测的结论可能潜藏着错误，未必正确.3.要证明一个结论是错误的，举反例就是一种常用方法.检验数学结论的常用方法实验验证法例1 先观察再验证．(1)图①中实线是直的还是弯曲的？(2)图②中两条线段a与b哪一条更长？(3)图③中的直线AB与直线CD平行吗？解：观察可能得出的结论是：①实线是弯曲的；②a更长一些；③AB与DC不平行．而我们用科学的方法验证后发现：①实线是直的；②a与b一样长；③AB平行于CD.有时视觉受周围环境的影响，往往误导我们，让我们得出错误的结论，所以仅靠经验、观察是不够的，只有通过科学的实验进行严格的推理，才能得出最准确的结论．推理证明法例2 当n为正整数时，代数式(n2－5n＋5)2的值都等于1吗？解：当n＝1时，(n2－5n＋5)2＝12＝1；当n＝2时，(n2－5n＋5)2＝(－1)2＝1；当n＝3时，(n2－5n＋5)2＝(－1)2＝1；当n＝4时，(n2－5n＋5)2＝12＝1；当n＝5时，(n2－5n＋5)2＝52＝25≠1.所以当n为正整数时，(n2－5n＋5)2的值不一定等于1.方法总结:验证特例是判断一个结论错误的最好方法．... ... ...关键词：为什么要证明PPT课件免费下载，平行线的证明PPT下载，.PPTX格式； 本作品中主体文字及图片可替换修改，文字修改可直接点击文本框进行编辑，图片更改可选中图片后单击鼠标右键选择更换图片，也可根据自身需求增加和删除作品中的内容，源文件无水印。如认为该内容涉嫌侵权，可通过邮件提出书面通知，我们将及时处理。