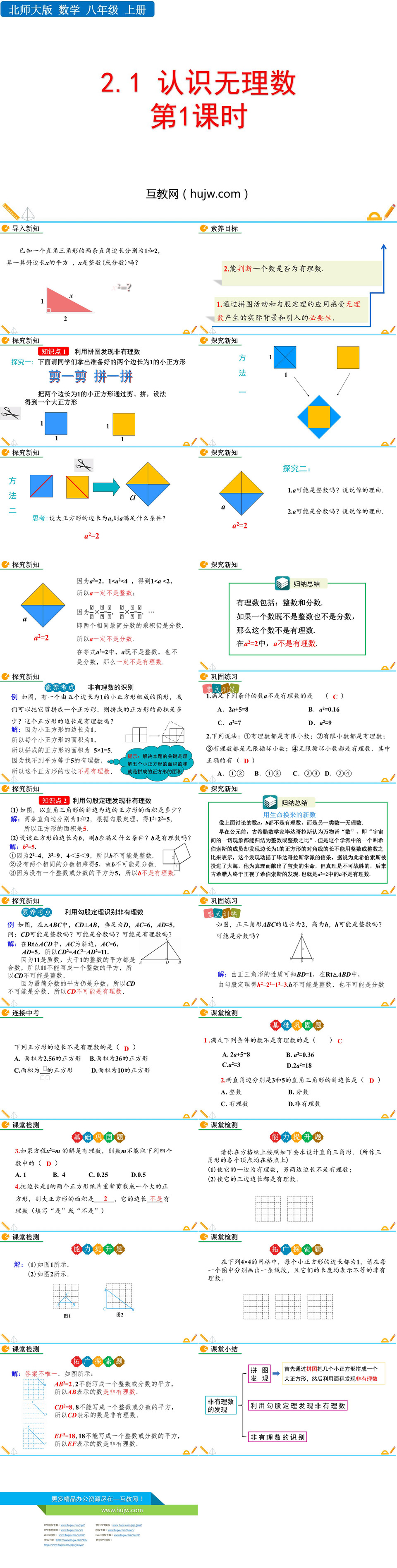
北师大版八年级数学上册《认识无理数》实数PPT免费下载(第1课时)，共24页。素养目标1.通过拼图活动和勾股定理的应用感受无理数产生的实际背景和引入的必要性．2.能判断一个数是否为有理数.探究新知利用拼图发现非有理数探究一: 下面请同学们拿出准备好的两个边长为1的小正方形把两个边长为1的小正方形通过剪、拼，设法得到一个大正方形归纳总结有理数包括：整数和分数.如果一个数既不是整数也不是分数，那么这个数不是有理数.在a2=2中，a不是有理数.非有理数的识别例 如图，有一个由五个边长为1的小正方形组成的图形，我们可以把它剪拼成一个正方形．则拼成的正方形的面积是多少？这个正方形的边长是有理数吗？解：因为小正方形的边长为1，所以每个小正方形的面积为1，所以拼成的正方形的面积为 5×1=5.因为找不到平方等于5的有理数，所以这个正方形的边长不是有理数．利用勾股定理发现非有理数(1)如图，以直角三角形的斜边为边的正方形的面积是多少？ 解：两条直角边分别为1和2，根据勾股定理，得12+22=5，所以正方形的面积是5.(2)设该正方形的边长为b，则b应满足什么条件？b是有理数吗？解：b2=5.①因为22=4，32=9，4＜5＜9，所以b不可能是整数.②没有两个相同的分数相乘得5，故b不可能是分数.③因为没有一个整数或分数的平方为5，所以b不是有理数.用生命换来的新数像上面讨论的数a，b都不是有理数，而是另一类数—无理数.早在公元前，古希腊数学家毕达哥拉斯认为万物皆“数”，即“宇宙间的一切现象都能归结为整数或整数之比”.但是这个学派中的一个叫希伯索斯的成员却发现边长为1的正方形的对角线的长不能用整数或整数之比来表示，这个发现动摇了毕达哥拉斯学派的信条，据说为此希伯索斯被投进了大海，他为真理而献出了宝贵的生命，但真理是不可战胜的，后来古希腊人终于正视了希伯索斯的发现.也就是a2=2中的a不是有理数.课堂小结首先通过拼图把几个小正方形拼成一个大正方形，然后利用面积发现非有理数利用勾股定理发现非有理数非有理数的识别... ... ...关键词：认识无理数PPT课件免费下载，实数PPT下载，.PPTX格式； 本作品中主体文字及图片可替换修改，文字修改可直接点击文本框进行编辑，图片更改可选中图片后单击鼠标右键选择更换图片，也可根据自身需求增加和删除作品中的内容，源文件无水印。如认为该内容涉嫌侵权，可通过邮件提出书面通知，我们将及时处理。